1）模型用法：

Black-Scholes模型是专门用于为欧式期权类金融衍生品定价的数学模型，一般可以简称为BS公式。普通用户可以使用BS公式对期权类产品进行理论的价值估算，并与市场价格进行对比，为投资提供参考。期权发行方可以利用BS公式计算期权的上架价格。

2）模型形式
欧式看涨期权BS公式

欧式看跌期权BS公式

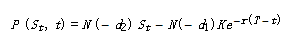
其中，CSt,t和PSt,t代表欧式看涨期权价格和欧式看跌期权价格，St代表t时刻标的资产的价格，K代表履约价格，T代表期权的到期日期，r代表无风险利率，一般用国债收益率和银行同业拆解利率代替, σ代表标的资产的波动率，t代表当前时刻。

d1和d2是模型参数，表达式如下：

3）基于BS公式的希腊字母

由于BS公式提供了欧式期权价值解析形式的表达式。所以，可以通过BS公式计算期权价值对各个参数的偏导数，即可以通过BS通过获取欧式期权希腊系数的解析表达式。

其中N'代表一元正态分布的概率密度函数。借助于期权的希腊字母表达式，可以对欧式期权价格变动与参数之间关系进行深入分析。欧式看涨期权的Delta系数永远大于0，欧式看涨期权价格随着标的资产价格增加而增加。欧式看跌期权的Delta系数永远小于0，欧式欧式看跌期权价格随着标的资产价格增加而减少。

4）Black-Scholes模型的推广看跌期权的价格随着标的资产增加而下降。欧式看跌期权和看涨期权的Gamma系数和Vega系数都大于零，说明欧式期权的价值都会随着标的资产波动水平的增加而增加。欧式看涨期权的Rho系数大于等于0，而欧式看跌期权的Rho系数小于等于0，说明欧式期权价格随着无风险利率增加而增加，而欧式看跌期权价格随着无风险利率增加而减小。

5）Black-Scholes模型的局限性
Black-Scholes模型有两个主要的局限性。第一，Black-Scholes模型只能用于欧式期权单资产金融衍生品价，无法为美期权、亚式期权和多资产期权定价；第二，Black-Scholes模型定价的有效性严重依赖于模型基础假设。当模型假设不成立或者部分不成立时，Black-Scholes模型确定的价格便是不准确的。

Black-Scholes模型要求标的资产价格每个时刻的价格是独立同分布的随机变量，无序列相关性，同时Black-Scholes模型也要求波动率和无风险利率是固定的，不存在异方差性和时变特征。在数字货币交易市场中，Black-Scholes模型所依赖的假设很难得到满足。一般而言，数字货币价格在不同时间点存在明显的概率分布异质性，并且存在突出的异方差性和序列相关性。在对以数字货币为标的的衍生产品定价时，需要对Black-Scholes模型进行调整，比如利用Levy过程代替布朗运动，用随机波动率模型、移动平均波动率和GARCH模型代替固定波动率。

使用Levy过程和随机波动率模型来改良Black-Scholes模型时，通常无法获取解析形式的期权价格表达式，并且需要使用数值解方式获取期权价格，对于一般投资者来说应用难度较大。建议使用普通投资者使用移动平均波动率和GARCH模型对Black-Scholes模型进行改良。用移动平均波动率和GARCH模型计算得到的时变波动率代替固定波动率，就可以得到Black-Scholes定价模型下时变期权价格。移动平均波动率计算较为简单，将波动率带入MA函数即可。投资者可以使用R语言和Python内部函数，利用标的数字货币收益率计算GARCH模型下的时变波动率。